(14)
SINTESI e COMPLEMENTI
Integrale Indefinito e Legge Assoluta
INTRODUZIONE
Questa RICERCA ha cercato di chiarire le principali proprietà di alcuni FLUIDI TERMODINAMICI (Liquidi, Gas, Miscugli), già ampiamente esaminati in una TESI di LAUREA avente per TITOLO: CRITERI di OTTIMAZIONE del RENDIMENTO di un MOTORE PRIMO TERMICO.
Abbiamo ottenuto RISULTATI apparentemente ANOMALI, non facilmente ACCETTABILI dai COMPETENTI, che li ritengono PRESUNTUOSI, non meritevoli di VERIFICA malgrado la dimostrazione MATEMATICA della loro presunta AUTENTICITA'. Sono nuovi Concetti di CATENA CINEMATICA, ENTROPIA, RENDIMENTO, VAPORE SATURO, DISTILLAZIONE, SECONDO PRINCIPIO, fino al MOTO PERPETUO di SECONDA SPECIE.
Infatti questi ARGOMENTI promettono RENDIMENTI UNITARI, nuovi conceti di ENTROPIA, di PRIMITIVA (integrale indefinito) e tant'ALTRO, terminando infine con una LEGGE SPERIMENTALE che assicura un CONTATTO SENSORIALE col MONDO ESTERNO.
1) MOTORI TERMICI E RENDIMENTI
Questi ATTRITI formano il RENDIMENTO INTERNO η0=(1-λA)(1-λC)≈0,85, che RIDUCE mediamente del 15% il RENDIMENTO η=L/Q dei CICLI IDEALI (Otto, Diesel, Joule, Carnot, ecc.) come confermano i rispettivi CICLI INDICATI dove gli SCAMBI Energetici di LAVORO LR e CALORE QR determinano il VALORE Sperimentale MEDIO del RENDIMENTO REALE ηR=LR/QR:
Questo VALORE approssimato di ηR≈0,85η può ritenersi ACCETTABILE soltanto nelle MACCHINE ROTATIVE, in particolare nelle TURBINE a GAS, ma niente affatto nelle MACCHINE ALTERNATIVE dove invece si OTTIENE un valore di ηR=LR/QR molto INFERIORE, come infatti risulta MISURANDO il LAVORO LR ottenuto intorno all’ALBERO e il CALORE QR speso nella CAMERA di COMBUSTIONE.
Inoltre tutti i CICLI TERMICI (Otto, Diesel, Joule, Carnot, ecc.) si svolgono a TEMPERATURE ELEVATE (T>Tc) e quindi, in prima approssimazione, seguono la TEORIA dei GAS PERFETTI, ignorando la COMBUSTIONE e il relativo RENDIMENTO ORGANICO.
In assenza di ALTERNATIVE, la DISCORDANZA dipende essenzialmente dalla DIVERSITA' delle due MACCHINE, cioè dalla CATENA CINEMATICA che COLLEGA la CAMERA di Combustione all’ALBERO, quasi INESISTENTE nelle TURBINE ma DETERMINANTE nei MOTORI ALTERNATIVI, azionati dal Meccanismo BIELLA-MANOVELLA.
Nelle Condizioni di REGIME (durante il moto), ogni MACCHINA TERMICA a Combustione Interna (alternativa, rotativa) AUTOGESTISCE in TEMPI REALI (istante per istante) il suo BILANCIO Energetico TERMICO (δQ≥0) e MECCANICO (δL≥0) con l’ESTERNO.
Insomma, la MACCHINA FUNZIONA da SOLA, in modo AUTONOMO, INDIPENDENTE, a “SCATOLA CHIUSA”. Quindi è certamente il MECCANISMO che determina le CAUSE Termodinamiche del MOTO, cioè gli SCAMBI ENERGETICI (δQ,δL) e il RENDIMENTO (η). Chi ALTRI se NO?
A parte gli ATTRITI (λA,λC) di cui la (1) TIENE CONTO ad esempio nel Piano Meccanico O(F,s), questo significa che la CATENA CINEMATICA crea il CICLO IDEALE ℑ nella CAMERA di COMBUSTIONE e poi lo TRASMETTE all’ALBERO trasformandolo in un CICLO INDOTTO ℑ*, aventi la STESSA AREA ma DIFFERENTI FORME.
Questi 2 Cicli corrrispondenti ℑ⇔ℑ*, situati agli ESTREMI P,P* del MECCANISMO, compiono lo stesso LAVORO L=L*con differenti RENDIMENTI η≠η*. Ma il MOTORE è AZIONATO soltanto dal CICLO INDOTTO ℑ*, che potrebbe collocarsi in un ipotetico CILINDRO TOROIDALE intorno all’ALBERO, come nelle TURBINE, ignrando il resto della MACCHINA, come se non esistesse.
Sostituendo η→η* nella (1), si ottiene quindi il seguente valore approssimato del RENDIMENTO REALE EFFETTIVO ηE valido per ogni MACCHINA TERMICA a Combustione Interna:
Peraltro, lo STATO FISICO di una MASSA M(kg) di GAS (Ideale, Reale) risulta definito (Gibbs) da due VARIABILI INDOPENDENTI, di cui CONVIENE assumere la COPPIA p=F/A(Pa),V=As(m3) oppure F=Ap(N),s=V/A(m), LEGATE alla COSTANTE AREALE A(m2).
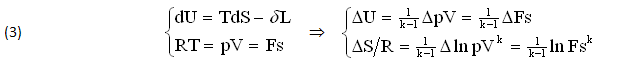
Ritornamdo all’Ipotesi di Ottimazzare i MOTORI TERMICI, si tratta di MODIFICARE opportunamente le rispettive CATENE CINEMATICHE, cioèi Meccanismi che collegano la CAMERA di COMBUSTIONE all’ALBERO, allo scopo di migliorare il RENDIMENTO INDOTTO η*∈ℑ* che figura nell’EQUAZIONE (2), applicando le FUNZIONE di STATO (3) ed altre EQUAZIONI dello stesso tipo.
In tal modo l’Ottimazione del BILANCIO ENEGETICO (δQ,δL) diventa (in linea di principio) soltanto QUANTITATIVO, con MODESTI risultati nelle TURBINE, dove le (1),(2) sono POCO DIFFERENTI (η≈η*), ma NOTEVOLE nei MOTORI ALTERNATIVI, azionati dal Meccanismo BIELLA-MANOVELLA, dove i RENDIMENTI INDOTTI η* possono CRESCERE oltre il 30%, a volte SUPERANDO addirittura quelli η dei CICLI IDEALI ℑ svolti nei rispettivi CILINDRI.
C’è da aggiungere le VARIANTI del CICLO RANKINE-HIRN negli attuali IMPIANTI TERMICI a VAPORE, dove la CONDENSAZIONE può essere ARRESTATA quando si vuole sulla IsoTermoBarica (dT=0),(dp=0),(orizzontale) del VAPORE-SATURO, formando un nuovo PUBTO INIZIALE (O) dove, conformemente alla FUNZIONE di STATO φ(p,T,xO)=0, avviene l’Incremento ISOTERMICO di PRESSIONE (dT=0),(Δp>0), seguito dall’Incremento ISOBARICO di TEMPERATURA (ΔT>0),(dp=0) sulla ISOTITOLO (dx=0) passante per (O).
Questo accade anche nel CICLO RANKINE HIRN, dove il suo PRIMO LATO non si trova (come si crede) nella ZONA LIQUIDA e dalle cui VARIANTI abbiamo ottenuto i CICLI ENTALPICI e i CICLI ENTROPICI, ampiamente DESCRITTI in altre pagine del SITO.
Qui finisce la TESI sul Rendimento, ma poi senza volerlo la stessa Ricerca ha sconfinato nei settori più alti della FISICA TEORICA riguardanti i PRINCIPI DELLA TERMADINAMICA, generalmente ritenuti assolutamente validi (certi, intoccabili) pur essendo di natura prettamente sperimentale, mentre invece molti Studiosi nutrono cauti dubbi di affidabilità, specialmente sul SECONDO, sperando di ottenere conferme o smentite anche per via matematica, malgrado i numerosi risultati delle applicazioni, in apparenza (?) positive.
Si suppone infatti che l’ENTROPIA ottenuta dai Teoremi di CARNOT-CLAUSIUS rappresenti l’OMONIMO POSTULATO, cioè il SECONDO PRINCIPIO. In effetti costituisce un insolito DIFFERENZIALE dS=δQ/T legato (dal fattore integrante 1/T) al generico SCAMBIO TERMICO dQ¹0, che può diventare il DIFFERENZIALE dQ=δQ=TdS definito (dS=δQ/T)⇔(δQ=TdS) dalla stessa ENTROPIA dS=δQ/T, come risulta dalle EQUAZIONI (3). Perciò l’ENTROPIA non può rappresentare l’unica Espressione Matematica del SECONDO PRINCIPIO.
2) FORME INFINITESIME LINEARI, DIFFERENZIALI
Per chiarire i suddetti sconfinamenti e motivare quelle diffidenze, cominciamo col ricordare che poche GRANDEZZE FISICHE Z(x,y) si conoscono in TERMINI FINITI, come le (3). Generalmente si esprimono in TERMINI INFINITESIMI mediante FORME DIFFERENZIALI LINEARI del tipo dZ=X1dx1+X2dx2+…+Xndxn, che nel caso di 2 VARIABILI INDIPENDENTI (x,y) assumono la seguente ESPRESSIONE, dove i COEFFICIENTI X(x,y) e Y(x,y) vengono DEFINITI (per via sperimentale) in un CAMPO CONNESSO C⊆ℜ2, ∀(x,y)∈C:
Per conoscere (in termini finiti) alcuni VALORI della FUNZIONE INCOGNITA Z(x,y), occorre INTEGRARE δZ(x,y) lungo una determinata CURVA γ∈C di EQUAZIONI x=s(t),y=y(t), dal PUNTO INIZIALE t0∈γ al generico PUNTO FINALE t∈γ, assegnando i 2 coefficienti X(x,y),Y(x,y), la linea di Integrazione γ∈C, infine gli ESTREMI (t0,t)∈γ:
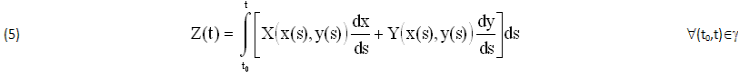
INFINITESIMI del tipo (4) sono gli SCAMBI TERMICI δQ≠0 e MECCANICI δL≠0, che in TEMPI REALI (istante per istante) DEFINISCONO i BILANCI ENERGETICI delle MACCHINE TERMICHE.
Peraltro, se entrambi i coefficienti X(x,y),Y(x,y) si assegnano in un CAMPO semplicemente CONNESSO (CSC), E⊆ℜ2, allora può accadere che ∀(x,y)∈E l’Infinitesimo δZ(x.y) diventi un Differenziale dZ(x,y), di cui (in linea di principio) deve ESISTERE almeno una PRIMITIVA INCOGNITA Z(x,y), REALE o COMPLESA, che lo SODDISFA:
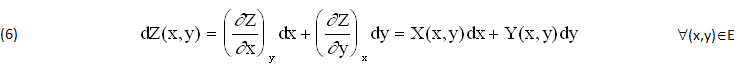
Generalmente, in ASSENZA di ALTERNATIVE, anche il DIFFERENZIALE (6) si risolve con INTEGRALI CURVILINEI del tipo (5), calcolabili per TENTATIVI e VERIFICHE di DERIVAZIONE, suppunendo che la PRIMITIVA INCOGNITA Z(x,y) ESISTE effettivamente, DIPENDE dai PUNTI (t0,t)∈E0 ma non dalla LINEA (γ∈E) che li CONGIUNGE.
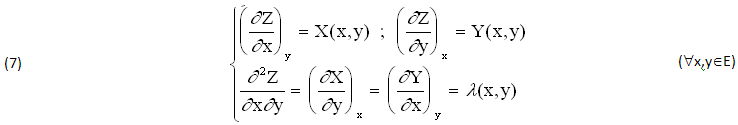
Viceversa, partendo da una FUNZIONE integranda ARBITRARIA λ(x,y)∈C0(E) possiamo CALCOLARE i seguenti COEFFICIENTI (8) X*(x,y), Y*(x,y) di un nuovo DIFFERENZIALE (8)1 dove COMPAIONO 2 FUNZIONI ARBITRAIE V(x),W(y) MONOVARIABILI, che supponiamo CONTINUE ∀(x,y)∈E, COSTANTI o NULLE:
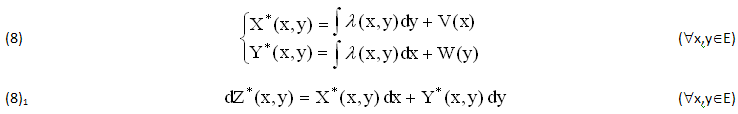
3) ALCUNE RIFLESSIONI
Facendo riferimento ai GAS IDEALI e senza escludere possibili ERRORI, abbiamo ottenuto RISULTATI alquanto INSOLITI. Perciò, prima di proseguire, anticipiamo 3 brevi RIFLESSIONI riguardanti: A) il Concetto di PRIMITIVA; B) il Concetto di ENTROPIA, C) i FLUIDI.
A) Il CONCETTO di LIMITE rappresenta l’ALGORITMO FONDAMENTALE di tutta l’ANALISI MATEMATICA, un preciso CALCOLO SISTEMATICO che trova la sua più naturale APPLICAZIONE nella DEFINIZIONE di DERIVATA.
In questi casi le 2 FUNZIONI ARBITRARIE V(x),W(y) MODIFICANO notevolmente il CONCETTO di PRIMITIVA Z*(x,y). Peraltro lo stesso INTEGRALE diventa MONOVARIABILE lungo qualsiasi LINEA γ∈E0∈ℜ2 di EQUAZIONE y=y(x)∈C0(E0), OTTENENDO una estesa CLASSE di PRIMITIVE ANOMALE Z(x), REALI e/o COMPLESSE con DERIVATE REALI, INCOMPATIBILI col TEOREMA di TORRICELLI.
y=y(x)∈C0(E0), OTTENENDO una estesa CLASSE di PRIMITIVE ANOMALE Z(x), REALI e/o COMPLESSE con DERIVATE REALI, INCOMPATIBILI col TEOREMA di TORRICELLI.
B) Il teoremi sperimentali di CARNOT-CLAUSIUS definiscono il ECONDO PRINCIPIO della TERMODINAMICA ma anche il DIFFERENZIALE dS=δQ/T di una strana FUNZIONE di STATO (link.02) chiamata ENTROPIA, che dovrebbe dimostrare la CERTEZZA MATEMATICA di quei TEOREMI, come risulta dalle seguenti EQUAZIONI (10):
Il RENDIMENTO η=L/Q delle MACCHINE TERMICHE PERFETTE, funzionanti secondo un CICLO di CARNOT invertibile, DIPENDE unicamente dalle due TEMPERATURE estreme (T1,T2):
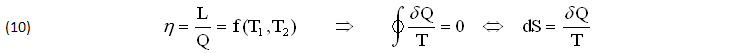
In questi casi limiti il RENDIMENTO REALE EFFETTIVO ηE=η0η* espresso dalla (2) assume all’INCIRCA lo stesso VALORE del RENDIMENTO INDOTTO η*∈ℑ*, ottenendo ηE=η*. Questo vale anche per la MACCHINA PERFETTA di CARNOT, dove il RENDIMENTO EFFETTIVO ηE=η definito dalla (10) DIPENDE anche dal MECCANISMO e DOVREBBE assumere un'ESPRESSIONE del tipo:
Di questi 2 PARAMETRI (μ,η*) occorre tener CONTO nella precedente DEFINIZIONE (10) di ENTROPIA, che invece li IGNORA e quindi non può rappresentare l’Unica Traduzione Matematica del SECONDO PRINCIPIO, cioè il suo unico STRUMENTO di MISURA.
Al più potrebbe costituire Condizione NECESSARIA (non Sufficiente) per la sua VALIDITA', ancora da Dimostrare. Questo significa che l’ESPRESSIONE (11) del RENDIMENTO EFFETTIVO ηE TOGLIE al SECONDO PRINCIPIO il concetto di ENTROPIA e quindi ogni possibilità di essere TRADOTTO in termini MATEMATICI, senza escludere le originarie AFFERMAZIONI del POSTULATO di CLAUSIUS:
il CALORE NON PASSA SPONTANEAMENTE dai CORPI FREDDI ai CORPI CALDI.
C) La REGOLA delle FASI (di Gibbs) assicura che lo STATO FISICO dei FLUIDI risulta DEFINITO da 2 variabili (x,y)∈E0⊆ℜ2, che determinano le sue FUNZIONI di STATO Zj∈∇ con EQUAZIONI del tipo Zj=fj(x,y) come nei precedenti esempi (3), dove l’ENERGIA INTERNA ΔU rappresenta il PRIMO PRINCIPIO mentre l’ENTROPIA ΔS nega la certezza MATEMATICA del SECONDO.
A questi risultati conducono i COEFFICIENTI X*(x,y), Y*(x,y) del DIFFERENZIALE (8)1, che definiscono la FORMA (8) del SISTEMA di STATO dei FLUIDI, cioè 2 EUAZIONI fra le 4 VARIABILI (x,y,X,Y), dove basta assegnare la FUNZIONE INTEGRANDA λ(x,y)≠0 affinchè nella PRIMITIVA Z*(x,y), espressa dall’INTEGRALE (9), compaiano due FUNZIONI ARBITRARIE V(x),W(y).
E’ strano che lo STUDIO di una estesa CLASSE di CORPI e FENOMENI si fonda sulla conoscenza di QUATTRO GRANDEZZE FISICHE (x,y,X,Y)∈E0⊆ℜ2 due delle quali risultano INDIPENDENTI, e che la STESSA REGOLA vale anche nei FENOMENI BIOLOGICI della VITA CELLULARE, dove il CODICE GENETICO del DNA PRODUCE varie Trasformazioni PERMUTANDO due a due le quattro MOLECOLE di BASE (A,G,C,T) che INCOLLANO i PIOLI TRASVERSALI della STRUTTURA ELICOIDALE: Forse la CONOSCENZA è prossima alla “TEORIA del TUTTO” (?).
4) PRIMITIVE ANOMALE
Due generiche FUNZIONI MONOVARIABILI X(x)∈C1(A),Y(y)∈C1(B), DEFINITE ∀(x,y)∈(A,B)⊆ℜ, formano i COEFFICIENTI del seguente DIFFERENZIALE dZ(x,y), che determina una CLASSE di PRIMIIVE Z(x,y)∈C2(A,B):
A differenza delL’INFINITESIMO (4), che rappresenta le TRASFORMAZIONI ottenute dagli INTEGRALI CURVILINEI (5), l’EQUAZIONE (12) costituisce un DIFFERENZIALE del tipo (6), definito ∀(x,y)∈(A,B)⊆(E), che secondo il Teorema di TORRICELLI-BARROW dovrebbe ammettere l’Unica PRIMITIVA INCOGNITA Z(x,y)∈C1(E) espressa dal seguente INTEGRALE INDEFINITO:
Tuttavia lo stesso DIFFERENZIALE (12) soddisfa alle CONDIZIONI (7) di INTEGRABILITA’, o di CHIUSURA, o di SCHWARZ, dove però risulta λ(x,y)=0. Esse DIMOSTRANO l’effettiva ESISTENZA della SOLUZIONE Z(x,y)∈C1(E) ma anche di altre Primitive Z*(x,y)∈C2(E) ottenute con l’Integrale Doppio (9), definite ∀(x,y)∈(E):
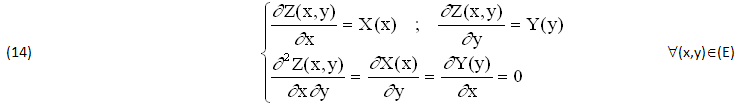
Infatti, una prima INTEGRAZIONE della EQUAZIONE ∂2Z/∂x∂y=0 conduce alla seguente PRIMITIVA INCOGNITA Z*(x,y)∈C2(E), dove le due FUNZIONI INTEGRANDE sono ARBITRARIE, V(x)∈C1(A), W(y)∈C1(B), che includono la PRIMITIVA (12) Z(x,y)∈C1(A,B) ponendo V(x)=X(x),W(y)=Y(y):
In particolare, se una delle due VARIABILI Indipendenti (x,y)∈(E) si suppone COSTANTE (k), ponendo ad esempio (y=k),(dy=0), allora ENTRAMBE le PRIMITIVE (13),(15) diventano MONOVARIABILI, ottenendo 2 distinte SOLUZIONI del Tipo seguente.

Le due SOLUZIONI (16) del differenziale (12), sembrano INCOMPATIBILI. Ci rendiamo conto quanto sia DIFFICILE accettare questi RISULTAI, ottenuti dal SISTEMA (7), dove l’INTEGRALE DOPPIO (8) della DERIVATA SECONDA MISTA ∂2Z*/∂x∂y=λ(x,y)=0 COLLOCA le FUNZIONI ARBITRARIE V(x),W(y) all’origine di questi DUBBI.
Un’altra CONFERMA proviene dall’INTEGRALE (15), supponendo di conoscere ∀(x,y)∈(E) i due COEFFICIENTI V(x)=f(x), W(y)=g(y) e le SOLUZIONI, ∫f(x)dx=F(x), ∫g(y)dy=G(y), affinché almeno la PRIMITIVA Z(x,y)∈C1(A,B) sia compatibile col TEOREMA di TORRICELLI:
Anche in questi casi restano VALIDE le seguenti PRIMITIVE, che risultano DIFFERENTI a causa delle 2 VARIABILI (x,y) ciascuna delle quali può diventare FUNZIONE ARBITRARIA dell’ALTRA, SOSTITUENDO ad esempio x=y(y) all’estremo superiore del PRIMO INTEGRALE ∫f(x)dx e/o y=j(x) all’estremo superiore del SECONDO ∫g(y)dy:
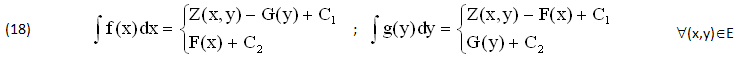
Nel complesso si tratta di PRIMITIVE Anomale INCOMPATIBILI col TEOREMA di TORRICELLI, anch’ ESSO poco AFFIDABILE in quanto RISOLVE soltanto i due DIFFERENZIALI f(x)dx e g(y)dy con ipotetiche Primitive ∫f(x)dx=F(x), ∫g(y)dy=C(y) ritenute ESISTENTI e UNIVOCHE ∀(x,y)∈(A,B), mentre INVECE risultano generalmente INCOGNITE in linea di Principio, essendo CALCOLABILI per TENTATIVI e ripetute VERIFICHE di DERIVAZIONE, con RISULTATI INCERTI.
Si tratta di ESEMPI Utili per confermare le (18) ma non necessari per la RICERCA, perciò possono IGNORARSI.
5) ESEMPI DI PRIMITIVE ANOMALE, utili ma non necessari per la RICERCA.
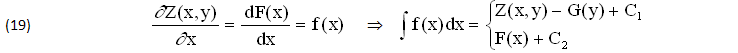
Esempi 1)
Consideriamo la seguente FUNZIONE TRIGONOMETRICA Z(x,y)∈C1(E), definita ∀(xy)≠1, la quale dipende da due VARIABILI (x,y)∈(E)⊆ℜ, di cui CALCOLIAMO le DERIVATE PARZIALI ∂Z/∂x, ∂Z/∂y, escludendo i PUNTI SINGOLARI xy=1 dove Z(x,y) subisce una DISCONTINUITA’ di PRIMA SPECIE con SALTO ΔZ(x,y)=±π:
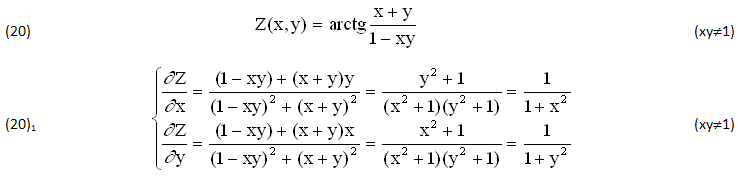
Le 2 VARIABILI INDIPENDENTI (x,y)∈(E) definiscono ∀xy≠1 la PRIMITIVA (20), quindi possiamo APPLICARE una di queste FUNZIONI INTEGRANDE, ad esempio f(x)=1/(1+x2), per esprimere le DUE PRIMITIVE (19):
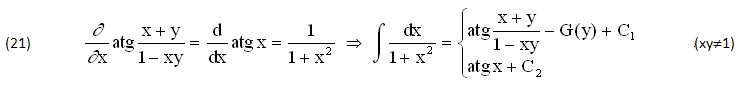
La stessa FUNZIONE (20) può ASSUMERE anche i seguenti VALORI, ∀(1-xy)>0 cioè ∀(xy<1):
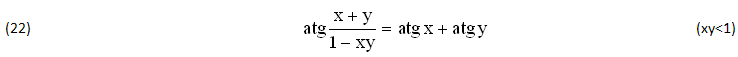
Essa SEMPLIFICA le applicazioni delle (21), ad esempio il seguente INTEGRALE DEFINITO dove le PRIMITIVE (J’,J”) risultano IDENTICHE (J’=J”),∀xy<1 oppure DIFFERENTI (J’¹J”),∀xy>1:
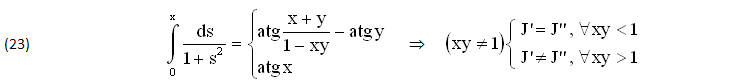
Una CONFERMA si ottiene ASSEGNANDO all’altra VARIABILE il valore COSTANTE y=k≠0:
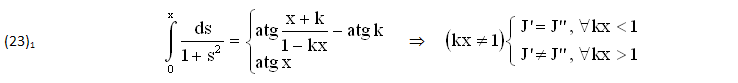
Un’altra VERIFICA (più interessante) si ottiene SOSTITUENDO all’estremo SUPERIORE x≠0 la FUNZIONE ESPONENZIALE x=(ey)/Y, ricordando (come abbiamo detto) che quella VARIABILE (x≠0) può diventare una FUNZIONE ARBITRARIA (Reale o Complessa) del tipo x=ψ(y), ∀y∈A:
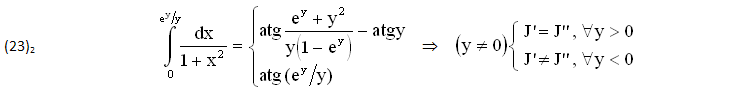
Fra gli altri ESEMPI dello stesso tipo (non riportati) è interessante il seguente CONFRONTO fra DUE PRIMITIVE certamente differenti (J’≠J”), una REALE, atgx , e l’altra COMPLESSA, atg(a+jb), ottenute dall’INTEGRALE (21) con la SOSTITUZIONE y=j/k, G(y)=0, definite ∀(k,x)≠0, facilmente VERIFICABILI per DERIVAZIONE:
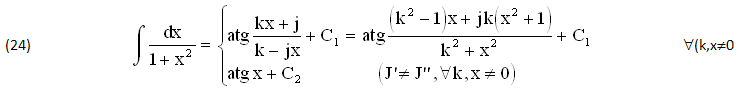
Esempi 2)
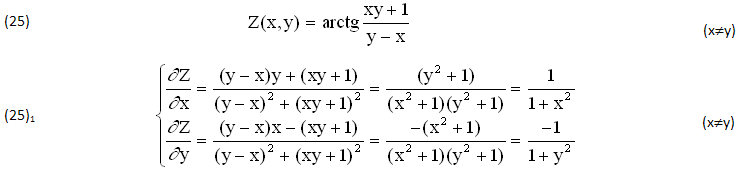
Applicando il PROCEDIMENTO (21), anche in questo caso possiamo PARTIRE dalla prima FUNZIONE INTEGRANDA f(x)=1/(1+x2) per RISALIRE alle due PRIMITIVE (19), anch’esse DEFINITE ∀(y-x)≠0 cioè ∀(x≠y):
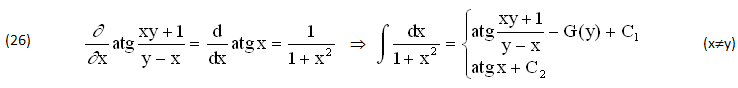
Peraltro l’equazione (25) può assumere anche i seguenti Valori, definiti ∀(y-x)>0 cioè ∀(x
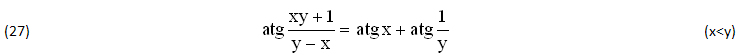
Quanto prima la (27) CONDIZIONA tutte le APPLICAZIONI delle (26), in particolare il seguente INTEGRALE DEFINITO ∀(x≠0), dove le PRIMITIVE (J’,J”) risultano IDENTICHE (J’=J”) ∀xy<1 o DIFFERENTI (J’≠J”) ∀xy>1:
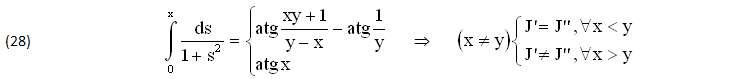
Un facile ESEMPIO come le (21)1 si ottiene ASSEGNANDO il valore COSTANTE y=k≠0:
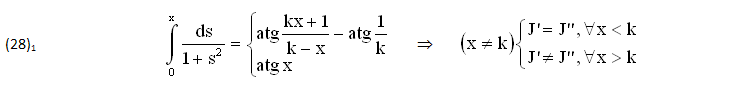
Anche in QUESTO caso, una VERIFICA si ottiene con la SOSTITUZIONE x=ey/y, ricordando che l’ESTREMO SUPERIORE (x) può diventare ARBITRARIO (Reale o Complesso) del tipo x=y(y):
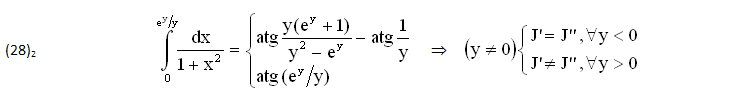
Infine applichiamo la versione COMPLESSA dell’INTEGRALE (26) ponendo y=jk, ∀(k,x)≠0:
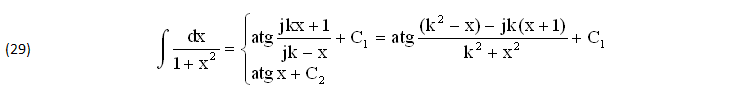
Esempi 3)
La seguente FUNZIONE TRIGONOMETRICA Z(x,y)∈C0(ℜ), definita ∀(x,y)∈ℜ, è dotata di CUSPIDI nei PUNTI SINGOLARI (x=y), come dimostrano le DERIVATE ∂Z/∂x, ∂Z/∂y definite ∀(x≠y), di cui per brevità OMETTIAMO i CALCOLI, alle quali il FATTORE UNITARIO λ=(y-x)/|y-x|=±1 assegna il DOPPIO SEGNO ALGEBRICO (±):
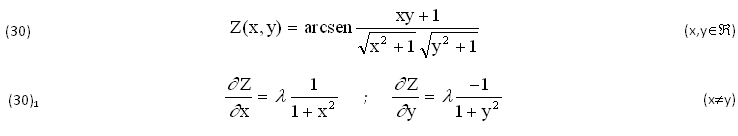
Anche il DIFFERENZIALE dZ(x,y) della FUNZIONE (30) viene CONDIZIONATO dal FATTORE λ=(y-x)/|y-x|=±1, spostando il DOPPIO SEGNO algebrico (±) nelle sue DERIVATE ∂Z/∂x, ∂Z/∂y, anch’esse DEFINITE ∀(x≠y):
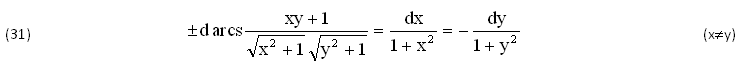
Come nei precedenti ESEMPI, possiamo scegliere la prima FUNZIONE INTEGRANDA f(x)=1/(1+x2) per ottenere le due PRIMITIVE (J’,J”) dell SISTEMA (19), le quali risultano IDENTICHE (J’=J”) ∀(x<y) oppure DIFFERENTI (J’≠J”) ∀(x>y), anch’ESSE CONDIZIONATE dal FATTORE UNITARIO l=(y-x)/|y-x|=±1 e DEFINITE ∀(x≠y):
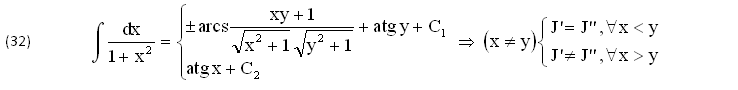
Assegnando alla y∈ℜ il valore COSTANTE y=k∈ℜ, (dy=0), come nelle (28)1 si OTTIENE:
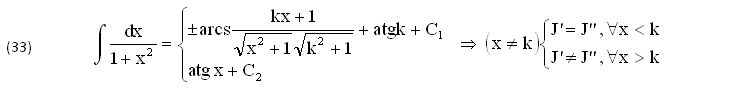
Infine (per brevità) ci limitiamo a SOSTITUIRE nella (32) il NUMERO IMMAGINARIO (y=jk),(k∈ℜ), ottenendo le seguenti PRIMITIVE, una COMPLESSA ∀(x,k∈ℜ) e l’altra REALE ∀(x∈ℜ), certamente DIFFERENTI ∀(x,k∈ℜ):
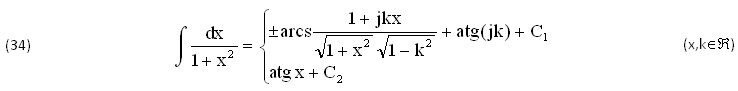
Esempi 4)
La seguente FUNZIONE f(x)∈C0(ℜ) è CONTINUA ∀x∈ℜ, come risulta dai LIMITI per x→(0,±∞):
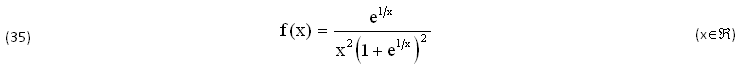
Secondo il TEOREMA di TORRICELLI la Funzione INTEGRANDA (35) dovrebbe ammettere un’UNICA PRIMITIVA F(x)∈C1(ℜ), ∀x∈ℜ. Ma il suo CALCOLO (per tentativi e verifiche di derivazione) conduce invece al seguente INTEGRALE F(x) dove RISULTA F(±∞)=1/2 mentre nell’ORIGINE (x=0) presenta una DISCONTINUITA’ di PRIMA SPECIE con SALTO ΔF(0)=-1, come dimostrano i suoi LIMITI. Peraltro non esistono altre Primitive della Funzione (35), nemmeno quella di TORRICELLI, continua F(x)∈C1(ℜ), ∀x∈ℜ:
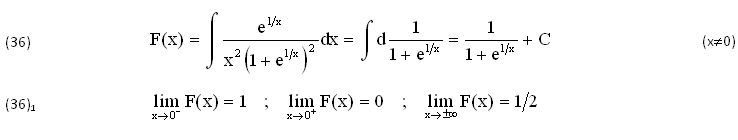
Sconvolgente CONCLUSIONE
6) RIFLESSIONI sul CONCETTO di PRIMITIVA
Il concetto di LIMITE è fondamentale per l’ANALISI MATEMATICA. Si tratta di un preciso CALCOLO SISTEMATICO che nel caso di una sola VARIABILE (∀x∈A⊆ℜ) serve a definire la DERIVATA f(x)∈C0(A) di una FUNZIONE CONTINUA F(x)∈C1(A) tramite il seguente RAPPORTO INCREMENTALE ΔF(x)/Δx per Δx→0.
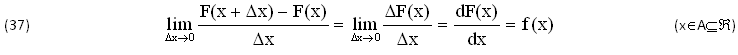
Viceversa, in MANCANZA della OPERAZIONE inversa di INTEGRAZIONE f(x)→F(x), la PRIMITIVA INCOGNITA F(x) si ESPRIME in Termini INFINITESIMI sostituendo il LIMITE (37) con la seguente EQUAZIONE DIFFERENZIALE, che si RISOLVE soltanto per TENTATIVI e ripetute VERIFICHE di DERIVAZIONE, senza alcuna CERTEZZA della sua ESISTENZA, malgrado la GARANZIA espressa dal TEOREMA di TORRICELLI-BARROW:
Tuttavia da questo INFINITESIMO si può risalire all’INCREMENTO ΔF= F(b)-F(a) con la seguente SOMMATORIA Σfj(x)Δjx, chiamata INTEGRALE di RIEMANN, che divide l’intero INTERVALLO (a≤x≤b) in una SERIE di Sottoinsiemi (Δjx>0) ridotti a INFINITESIMI (Δjx→0) che dipendono dai VALORI EFFETTIVI di (Δjx>0)∈(a≤x≤b):
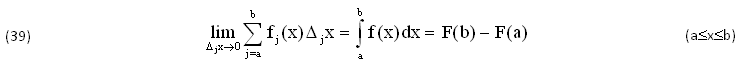
Peraltro il TEOREMA di TORRICELLI-BARROW risolve formalmente il DIFFERENZIALE (38) sostituendo quella SOMMATORIA Σfj(x)Δjx col SIMBOLO di INTEGRALE ∫f(x)dx, che pur restando INCOGNITO dovrebbe significare: SOMMA di INFINITI TERMINI INFINITESIMI, equivalente alla operazione INVERSA della DERIVATA. Invece lo stesso TEOREMA DIMOSTRA (in modo poco convincente) che ∀(a,x)∈A ogni FUNZIONE f(x)∈C0(A) ammette un’UNICA PRIMITIVA, REALE, COMPLESSA o INCOGNITA F(x)∈C1(A), avente la seguente ESPRESSIONE:
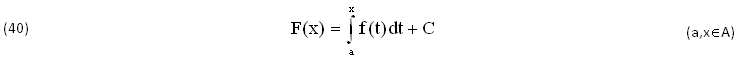
Ma la VERITA' è ben DIFFERENTE, come DIMOSTRANO le Condizioni di SCHWARZ (7) e le conseguenti soluzioni ARBITRARIE ∀(x,y)∈E, di cui riportiamo l’INTEGRALE doppio (9) ΔZ*(x,y) supponendo di CONOSCERE V(x),W(y) e la PRIMITIVA incognita Z*(x,y)∈C2(E) che include anche l’INTEGRALE di TORRICELLI (40) ∀(y=k),(dy=0):
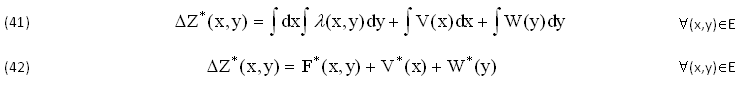
Da queste EQUAZIONI possiamo ottenere due differenti PRMITIVE della stessa FUNZIONE INTEGRANDA V(x), la prima delle quali risulta addirittura ARBITRARIA a causa della VARIABILE y∈E, anche perchè (come abbiamo detto) l’ESTREMO SUPERIORE dell’INTEGRALE potrebbe SOSTITUIRSI con FUNZIONI ARBITRARIE del tipo x=μ(y), tenendo conto che (in alternativa) la PRIMA SOLUZIONE può presentare DISCONTINUITA' di PRIMA SPECIE nei PUNTI y=k∈E:
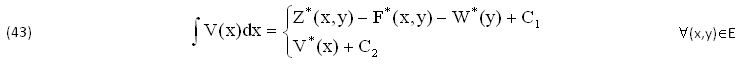
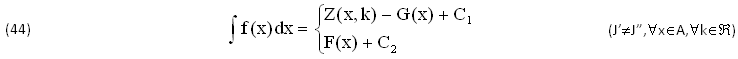
Il PROBLEMA si complica nelle EQUAZIONI di ORDINE n≥2, f(x,y',y'',.,y(n))=0, il cui INTEGRALE GENERALE y(x,k1,k2,..,kn) dipende da n COSTANTI ARBITRARIE. Ancor più nelle EQUAZIONI alle DERIVATE PARZIALI, che nel caso più semplice di n=2 VARIABILI Indipendenti, ∀(x,y)∈(A,B), si prestano allo STUDO della TERMODINAMICA dei FLUIDI (liquidi, gas, miscugli) e di altri fenomeni bivariabili, quando l’INTEGRALE diventa un SISTEMA di STATO del tipo (8), con 2 FUNZIONI ARBITRARIE V(x),W(y) di cui ci occuperemo.
7) IL SISTEMA DI STATO DEI FLUIDI
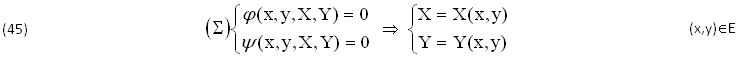
Inlinea di principio, basta dunque ASSEGNARE una generica COPPIA INDIPENDENTE (x,y)∈E, in un CAMPO Semplicemente CONNESSO (CSC)=E∈ℜ2, per definire il SISTEMA di STATO (Σ) e quindi anche i due COEFFICIENTI X(x,y),Y(x,y) del seguente DIFFERENZIALE, al quale (come abbiamo detto e di cui parleremo fra poco) occorre AGGIUNGERE altri VINCOLI per assicurare l’ESISTENZA della PRIMITIVA INCOGNITA Z(x,y)∈C2(E):
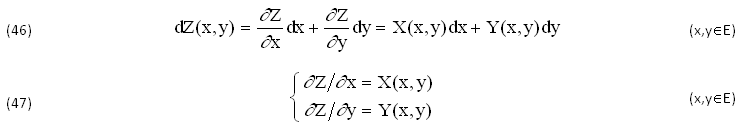
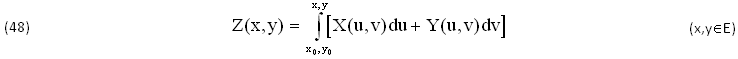
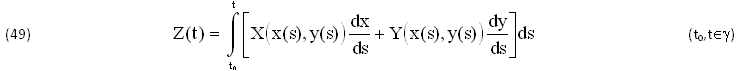
Queste soluzioni potrebbero NON ESISTERE o essere PLURIMERE. Infatti, assieme al (CSC), l’effettiva Esistenza della PRIMITIVA INCOGNITA Z(x,y)∈C2(E) ∀E∈ℜ2 RICHIEDE che siano SODDISFATTE anche le CONDIZIONI di SCHWARZ (7), dove risulta λ(x,y)≠0 e quindi VALGONO le seguenti EQUAZIONIi DIFFERENZIALI:
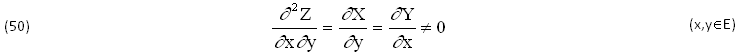
Si tratta di uno dei più semplici SISTEMI DIFFERENZIALI del 2O ORDINE alle DERIVATE PARZIALI, che in questo caso equivale al DIFFERENZIALE (46) e al SISTEMA di STATO (47) in quanto ESPRIME la stessa PRIMITIVA INCOGNITA Z(x,y)∈C2(E) di quel FLUIDO, definita ∀(x,y)∈E.
Viceversa, il DIFFERENZIALE (46) e il SISTEMA di STATO (47) si possono ottenere assegnando la funzione di SCHWARZ λ(x,y)∈C0(E), cioè la DERIVATA SECONDA MISTA ∂2Z/∂x∂y=∂2Z/∂y∂x del SISTEMA (50), ottenendo le seguenti condizioni di INTEGRABILITA’ GENERALIZZATA:
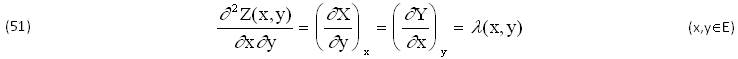
Assegnare la FUNZIONE di SCHWARZ λ(x,y)∈C0(E) significa assegnare il SISTEMA di STATO (45) (X,Y)∈C1(E) di un determinato FLUIDO di RIFERIMENTO. A differenza delle EQUAZIONI (50) che ASSICURANO soltanto l’ESISTENZA di una PRIMITIVA INCOGNITA Z(x,y), il nuovo SISTEMA (51) definisce anche il DIFFERENZIALE (46), cioè i 2 COEFFICIENTI (47) del SISTEMA di STATO X(x,y),Y(x,y) e l’INTEGRALE DOPPIO della PRIMITIVA Z(x,y)∈C2(E), legati alla FUNZIONE di SCHWARZ λ(x,y)∈C0(E) ma soprattutto alle due FUNZIONI ARBITRARIE V(x),W(y), da UTILIZZARE nei modi più opportuni:
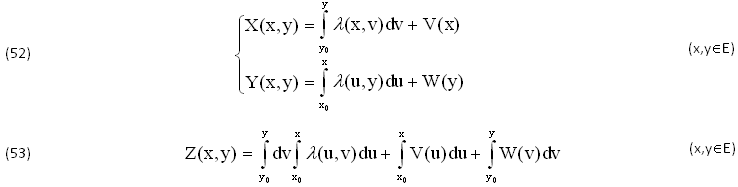
QUALCHE RITOCCO
A questo punto conviene tener conto dei seguenti SISTEMI DIFFERENZIALI EQUIVALENTI, il primo ottenuto differenziando il SISTEMA di STATO (52) e l’altro SOSTITUENDO ALCUNI dei suoi TERMINI. In tal modo i rispettivi COEFFICIENTI facilitano il CALCOLO immediato delle DERIVATE PARZIALI fra le 4 VARIABILI (x,y,X,Y):

Cme abbiamo detto, queste EQUAZIONI semplificano il CALCOLO delle DERIVATE PARZIALI fra le 4 VARIABILI (x,y,X,Y), definite dai RAPPORTI fra i rispettivi DIFFERENZIALI dx,dy,dX,dY. In particolare, le 4 COPPIE INDIPENDENTI (x,y),(x,Y),(y,X),(X,Y) definiscono le 8 DERIVATE seguenti, che abbiamo ASSOCIATO due a due allo scopo di ottenere 4 CONDIZIONI di INTEGRABILITA' EQUIVALENTI, a cominciare dalla (50).
Queste EQUAZIONI rappresentano 4 SISTEMI EQUIVALENTI e le rispettive PRIMITIVE INCOGNITE, che nel caso dei FLUIDI formano i 4 POTENZIALI TERMODINAMICI della CHIMICA-FISICA, di cui ci occuperemo in seguito:
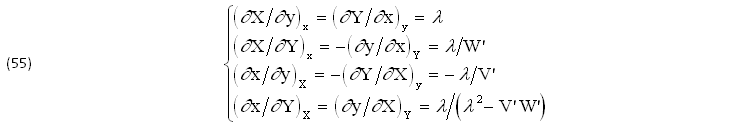
Quanto precede si SEMPLIFICA assegnando alla FUNZIONE di SCHWARZ λ(x,y) la COSTANTE λ=k∈ℜ. In questo caso il SISTEMA di STATO (52) assume la seguente FORMA RIDOTTA:
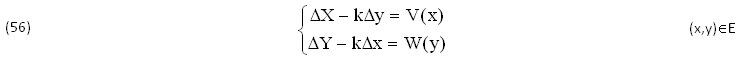
OSSERVAZIONE
Potrebbe nascere qualche DUBBIO sulla CORRISPONDENZA fra l’INFINITESIMO (46) e il DIFFERENZIALE (51), che produce i SISTEMI di STATO (52),(56). Peraltro quei RISULTATI li abbiamo ottenuti IGNORANDO (come se non esistesse) la FUNZIONE di SCHWARZ λ(x,y)≠0, introdotta soltanto nelle CONDIZIONI di CHIUSURA (51). Infatti le 3 FUNZIONI arbitrarie λ(x,y),V(x),W(y) RICOMPAIONO, assieme ai SISTEMI di STATO (52),(56), INTEGRANDO manualmente il DIFFERENZIALE (46), tramite un laborioso procedimento che per brevità omettiamo. Comunque quei SISTEMI di STATO (52),(56) assumono importanza nella TERMODINAMICA dei FLUIDI ma soprattutto in questa RICERCA, il cui COMPITO è quello di determinare l’effettivo significato MATEMATICO delle tre FUNZIONI ARBITRARIE λ(x,y),V(x),W(y), in particolare la CAPACITA' di interpretare le GRANDEZZE FISICHE ATTRIBUITE ai CORPI materiali. Alla FINE (come vedremo) ESSE DIVENTERANNO una autentica “LEGGE ASSOLUTA DELLA NATURA”.
8) IL PRIMO PRINCIPIO DELLA TERMODINAMICA
Nelle COORDINATE dei GAS IDEALI conviene INCLUDERE le tre GRANDZZE FISICHE: PRESSIONE (p>0),(N/m2), VOLUME SPECIFICO (v>0),(m3/kg) e TEMPERATURA (T>>Tc),(oK), che definiscono l’EQUAZIONE di STATO pv=RT ma anche i due CALORI SPECIFICI (cp,cv),(J/kgoK), tenendo conto delle due COSTANTI FISICHE R(J/kgoK) e k(ad), come risulta dalle seguenti EQUAZIONI sperimentali di MAYER, GAY-LUSSAC, JOULE:
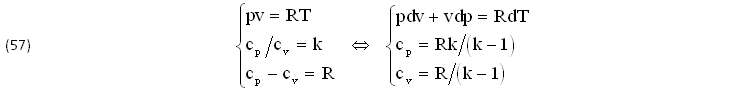
A causa delle 2 COSTANTI (R,k), anche quei due CALORI SPECIFICI (cp,cv) risultano praticamene COSTANTI. E’ questa la PROPRIETA’ più IMPORTANTE dei GAS IDEALI, soprattutto perchè le EQUAZIONI (57) si possono ESTENDERE con sufficiente APPROSSIMAZIONE ai GAS REALI, addirittura a TUTTI i FLUIDI TERMODINAMICI (Liquidi, Gas, Miscugli) IMPIEGATI nelle MACCHINE TERMICHE a COMBUSTIONE INTERNA, negli INTERVALLI.
Peraltro, acquista notevole importanza lo SCAMBIO Energetico con l’ESTERNO, cioè il CALORE ASSORBITO (Q) e il LAVORO CEDUTO L(J/kg), entrambi INCOGNITI in quanto DIPENDONO dalle TRASFORMAZIONI e quindi ASSUMONO le seguenti FORME INFINITESIME (δQ,δL), sciegliedo la COPPIA (p,v)>0:
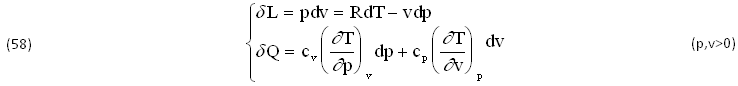
Tenendo conto delle EQUAZIONI (57) e dei VALORI MEDI delle due COSTANTI (R,k), si RICAVANO facilmente le seguenti tre ESPRESSIONI dello SCAMBIO TERMICO (δQ), DEFINITE ∀(p,v)>0:
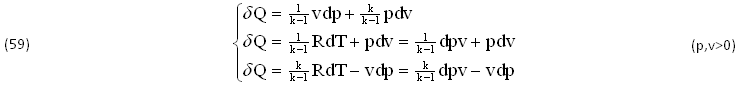
DIVIDENDO membro a membro per la TEMPERATURA T e tenendo conto dell’EQUAZIONE di STATO pv=RT, si ottiene il DIFFERENZIALE dell’ENTROPIA dS=δQ/T nelle seguenti FORME EQUIVALENTI, con l’immediata INTEGRAZIONE in Termini Finiti ΔS=(S-S0), anch’ESSE DEFINITE dalle 3 COPPIE INDIPENDENTI (p,v),(T,v),(T,p):
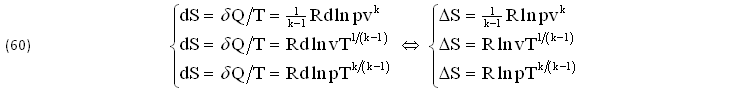
PAUSA RIFLESSIVA
Come l’ENERGIA INTERNA e l'ENTALPIA, anche l’ENTROPIA dS=δQ/T costituisce dunque una comune FUNZIONE di STATO, pur essendo inizialmente DEFINITA dal Teorema di CARNOT-CLAUSIUS che rapppresenta il SECONDO PRINCIPIO, fondato essenzialmente sulla presunta IRREVERSIBILITA' dei FENOMENI REALI, che tuttavia viene completamente IGNORATO (come se non esistesse) dalla sua effettiva DEFINIZIONE (60).
Di conseguenza quella FUNZIONE di STATO (dS=δQ/T) non può rappresentare l’ESPRESSIONE Matematica del SECONDO PRINCIPIO, la sua TRADUZIONE ANALITICA, la certezza della sua EFFETTIVA VALIDITA', nemmeno nelle CONDIZIONI di INVERTIBILITA' (dS=δQ/T)⇔(δQ=TdS) quando anche lo SCAMBIO TERMICO diventa un DIFFERENZIALE (δQ=dQ=TdS).
Questo (δQ=dQ=TdS) accade nelle TRASFORMAZIONI ISOCORE (dv=0) e/o ISOBARICHE (dp=0) dei CICLI-HIRN-ENTALPICI, dove lo SCAMBIO TERMICO (δQ) equivale alla ENERGIA-INTERNA (δQ)v=(dU)v e/o alla ENTALPIA (δQ)p=(dH)p, tenuto conto che neanche il CICLO di CARNOT (Invertibile) non può CONFONDERSI (link.08) col MOTORE TERMICO che lo GGESTISCE.
Analogamente, ripartendo dagli SCAMBI TERMICI (δQ) definiti delle (59), la DIFFERENZA (δQ-pdv) ricavata dalla SECONDA Equazione e la SOMMA (δQ+vdp) ottenuta dalla TERZA, determinano i DIFFERENZIALI della ENERGIA INTERNA (dU) e della ENTALPIA (dH), anch’ESSI calcolabili con immediata INTEGRAZIONE in Termini Finiti (ΔU,ΔH), due FUNZIONI di STATO legate alla COPPIA (p,v) oppure soltanto alla TEMPERATURA (T):
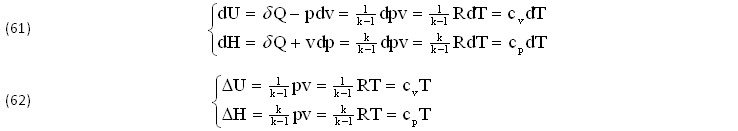
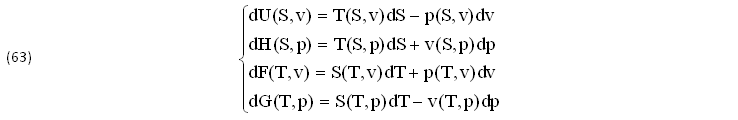
L’ENERGIA INTERNA dU=dQ-dLu e l’ENTALPIA dH=dQ+dLe definite dalle EQUAZIONIi (61) rappresentano due DIVERSI MODI per esprimere lo SCAMBIO energetico, TERMICO dQ e MECCANICO dL, che aziona ogni MOTORE, chiamando LAVORO INTERNO dLu=pdv e LAVORO ENTALPICO dLe=vdp i 2 INFINITESIMI (pdv) e (vdp).
Si tratta di due differenti ESPRESSIONI (dU=dQ-dLu),(dH=dQ+dLe) del PRIMO PRINCIPIO della TERMODINAMICA, molto UTILI nelle Trasformazioni dei Cicli TERMICI (Hirn, Entalpici, Entropici, Joule, Otto, Diesel, ecc.) e rappresentano due dei 4 POTENZIALI TERMODINAMICI impiegati nella CHIMICA-FISICA, che sono: l’ENERGIA INTERNA (dU=TdS-pdv), l’ENTELPIA (dH=TdS+vdp), l’ENERGIA LIBERA di HELMHOLTZ (dF=dTS-dU), l’ENERGIA LIBERA di GIBBS (dG=dTS-dH).
Vengono ESPRESSI dai 4 DIFFERENZIALI (dU),(dH),(dF),(dG) in funzione delle 4 COPPIE INDIPENDENTI (S,v),(S,p),(T,v),(T,p) del gruppo (p,v,T,S), ricavabili dal SISTEMA (61) sostituendo alcuni termini dei secondi membri:
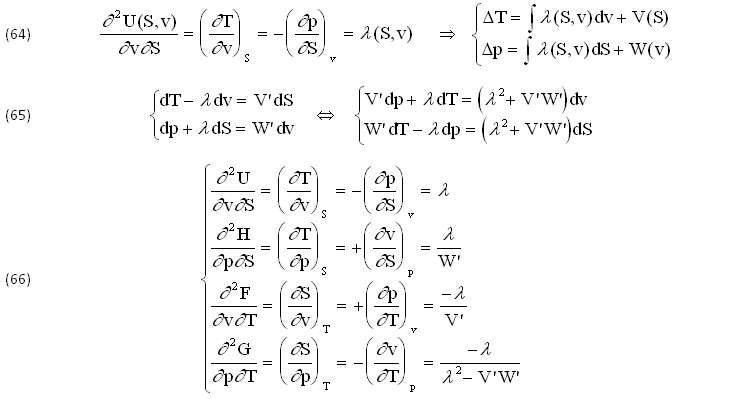
Anche in questo caso è facile OTTENERE i rispettivi SISTEMI di STATO (52), RISOLTI in FORMA RIDOTTA (56) ponendo λ=k∈ℜ. Quelle ESPRESSIONI si rendono NECESSARIE quando occorrono almeno 2 dei 4 POTENZIALI TERMODINAMICI (66), ad esempio l’ENERGIA INTERNA (dU=TdS-pdv) e l’ENTALPIA (dH=TdS+vdp).
Se invece SERVE soltanto una sola GRANDEZZA Termodinamica BIDIMENSIONALE del tipo Z(x,y), definita ∀(x,y)∈E⊆(CSC), conviene PARTIRE dall’EQUAZIONE Differenziale di SCHWARZ (51) che si risolve con l’INTEGRALE DOPPIO (53), soprattutto tenendo conto del SISTEMA di STATO (52) in Termini Finiti, espresso anche nella FORMA RIDOTTA (56).
Questo PROCEDIMENTO (che applicheremo in seguito) IGNORA i PRINCIPI della TERMODINAMICA (come se non esistessero) e consente di GIUNGERE (come abbiamo detto) a quella VERITA' che rappresenta una autentica LEGGE ASSOLUTA DELLA NATURA.
PAUSA RIFLESSIVA
Ogni GRANDEZZA FISICA Z(x,y)∈C2(E), definita ∀(x,y)∈E⊆(CSC), rappresenta una FUNZIONE di STATO spesso INCOGNITA che si esprime tramite il DIFFERENZIALE dZ(x,y), sapendo che le CONDIZIONI di CHIUSURA ∂2Z/∂y∂x=∂X/∂y=∂Y/∂x assicurano la SOLUZIONE Z(x,y), in Termini Finiti, INTEGRANDO senza tener conto della FUNZIONE di SCHWARZ ∂2Z/∂y∂x=l(x,y)∈C0(E):
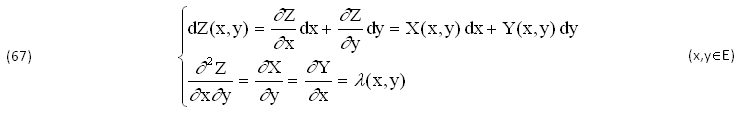
Infatti, generalmente si assegnano soltanto i due COEFFICIENTI X(x,y),Y(x,y)∈C1(E) IGNORANDO la FUNZIONE di SCHWARZ λ(x,y). Perciò il suo DIFFERENZIALE dZ(x,y) si RISOLVE per tentativi con INTEGRALI CURVILINEI Z(t) del tipo seguente, DEFINITI ∀(x,y)∈E e quindi COMPATIBILI col TEOREMA di TORRICELLI:
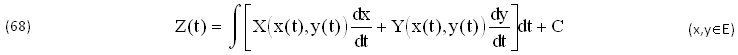
In alternativa conviene invece risolvere quei DIFFERENZIALI ∂2Z/∂x∂y=∂X/∂y=∂Y/∂x=λ(x,y) dopo avere assegnato in modo ARBITRARIO la FUNZIONE di SCHWARZ λ(x,y)∈C0(E), per ottenere il SISTEMA di STATO (52), che chiameremo (∑), e l’INTEGRALE DOPPIO (53) della nuova PRIMITIVA INCOGNITA Z(x,y)∈C2(E), dove assieme a λ(x,y) compaiono altre 2 FUNZIONI ARBITRARIE V(x),W(y), generalmente INCOMPATIBILI col TEOREMA di TORRICELLI. Con la Funzione di SCHWARZ λ(x,y)∈C0(E) si ottengono i RISULTATIi:
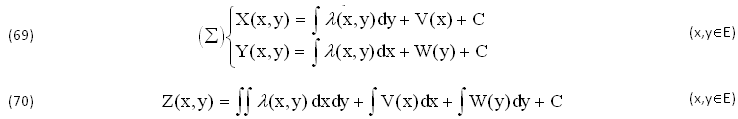
Geometricamente, gli INTEGRALI Z(t),(68) e Z(x,y) (70) FORMANO rispettivamente tutte le CURVE del PIANO O(x,y) e tutte le SUPERFICI dello SPAZIO-Tridimensionale O(x,y,z), mentre il SISTEMA di STATO (∑) rappresenta una SUPERFICIE dello SPAZIO quadrdimensionale W(x,y,X,Y) di EQUAZIONI Parametriche X=X(x,y),Y=Y(x,y).
Conviene dunque partire dal SISTEMA di STATO (∑) sperando di poter determina le FUNZIONI ARBITRARIE V(x),W(y) che dovrebbero rendere CONCRETE alcune APPLICAZIONI di (∑).
Il Problema è INVOLUTIVO, risolvibile SOLTANTO con l’IPOTESI di creare le CONDIZIONI SPERIMENTALI di V(x),W(y). A tale scopo, vediamo cosa accade esprimendo quel SISTEMA (∑) in FORMA DIFFERENZIALE (d∑), per poi riportarlo in TERMINI FINITI (∑') DIVIDENDO la PRIMA EQUAZIONE per dx≠0 e la SECONDA per dy≠0:
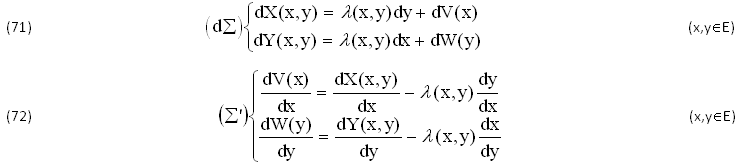
Nel nuovo SISTEMA di STATO (∑'),(72) la PRIMA EQUAZIONE DIPENDE soltanto da (x) e la SECONDA soltanto da (y). Infatti, la DERIVATA TOTALE dy/dx e la SUA INVERSA 1/(dx/dy) ammettono una PRIMITIVA ARBITRARIA f(x,y)=0 che lega le 2 VARIABILI (x,y)∈E di X(x,y),Y(x,y),λ(x,y), mentre ASSIEME alle altre due PRIMITIVE ARBITRARIE, φ(x,X)=0 di dX/dx e ψ(y,Y)=0 di dY/dy, FORMANO la CURVA (σ) dello SPAZIO Ω(x,y,X,Y).
Insomma, (∑') comprende 2 EQUAZIONI nelle 3 VARIABILI di cui (3-2)=1 risulta INDIPENDENTE, quindi rappresenta la CURVA (σ) dello SPAZIO quadridimensionale Ω(x,y,X,Y), definita dalla EQUIVALENZA (∑')⇒(σ):
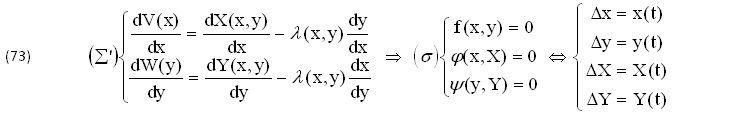
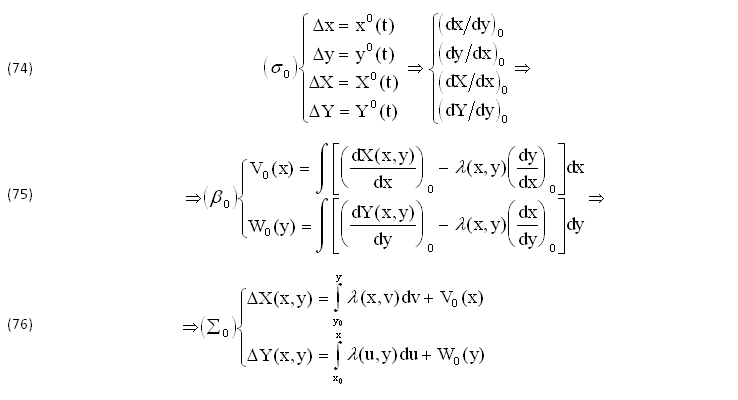
UN BREVE RIEPILOGO